Local Search: Simulated Annealing

Introduction

Local Search is a method that is used to solve optimization problems, where we are after a solution's state. Local search is a way to solve problems like vehicle routing, portfolio management, scheduling, and positioning problems without having to explore the entire searc space.

Simulated Annealing, which gets its name form the material sciences and working with metal, where annealing is the process of controlled cooling of a metal to make it more workable and have fewer defects.

The Simulated Annealing algorithm keeps a sort of temperature that decreases over time according to a schedule specified by the algorithm designer, and along with our evaluation function we look at how much worse or better our alternative solutions are. We then allow according to our "temperature", \(T\) and the measurement of change in our heuristic evaluation \(\Delta h\), we determine with some probability whether to accept this new move.

In turn this has a tendency to allow bad moves early on and eliminate them entirely later in the search. Imagine that the algorithm is considering a search space that has many local maxima, allowing less optimal moves, may allow the algorithm to escape the local maxima and achieve a better solution.

In the algorithm, Simulated Annealing picks a random move instead of a the best. If the move is an improvement, then the move will always be accepted. If the move is better, then the move will be accepted with a probability exponentially dependent on the change in our heuristic evaluation function \(\Delta H\) and Temperature \(T\).

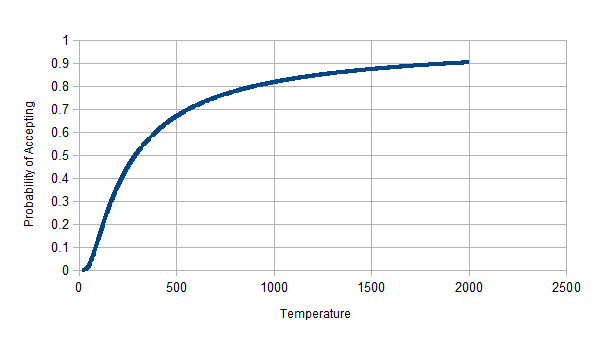
Below is a graph of what our exponential probability would look like for \(e^{(\frac {\Delta H}{T})}\) with \(T\) starting at 2000 and decreasing by 10 after each unit of time, and a fixed \(\Delta H = -200\). The graph shows how the \(-200\) move is less likely to be accepted as time goes on and \(T \rightarrow 0\).

Simulated Annealing Algorithm

Below is the Simulated Annealing Algorithm, which is derived from the pseudocode in AIMA by Russell & Norvig.

#Pseudo-Code

def accept(change, T):
    # Return boolean with probability e^(change/T)
    # (change / T) ~ 0 early on, increasing over time and rejecting negative moves later on.

def simulatedAnnealing(state,temperatureSchedule):
    current = state
    for (t = 1;; t++):
        T = temperature(t) # Tempreature at time t
        if T = 0
            return current
        next = generateNewState();
        change = next.value - current.value
        if change > 0
            current = next
        else
            current = accept(change, T) ? next : current

Additional References

Artificial Intelligence a Modern Approach
Simulated Annealing
Local Search