
Solving the N-Queens Problem with Local Search
JavaScript: Random Restart Hill Climbing
December 11, 2013
The Problem
The N-Queens problem is well known and well solved one in computer science. The rules are simple, given a chess board of size \(N \times N\), and \(N\) queens, find a placement for all \(N\) queens such that there is no queen that attacks any other queen.
Solving this by trying all possible configurations would me that we would have to explore \(64!\) combinations, which sounds terribly unreasonable, but if you think about the \(N\) queens, you will notice that each one has to be in a different column, and so we can encode our board onto an array of \(N\) elements, with each element in the range of \([1,N]\). And even then we would have to explore, \(N\) possible values for \(N\) positions, giving us \(N^N\) nodes to explore in the worst case in order to find a solution.
Below is a JavaScript implementation that uses Random Restart Best First Hill Climbing to reach a solution for a given \(N\) Queens problem.
If the algorithm gets stuck, it restarts from a random state, and tries again, and again until a solution is found.
Some alternative algorithms to solve N-Queens include other types of local search like, simulated annealing, backtracking, and constraint satisfaction algorithms.
// Count the number or row collisions
var rowCollisions = function (a) {
collision = 0;
for (var i in a) {
for (var j in a) {
if (j != i) {
collision = a[i] == a[j] ? collision+1 : collision;
}
}
}
return collision;
};
// Count the number of column collisions
var diaCollisions = function (a) {
collision = 0;
for (var i in a){
for (var j in a){
if (i != j) {
dp = Math.abs(i-j);
collision = a[i] == a[j]+dp ? collision+1 : collision;
collision = a[i] == a[j]-dp ? collision+1 : collision;
}
}
}
return collision / 2;
};
// Heuristic Evaluation Function for N Queens
// We will want to minimize collisions -- also referred to as min-conflicts in general
var evaluate = function (s) {
return diaCollisions(s) + rowCollisions(s);
};
// Generate a set of candidates.
var generateCandidates = function(current) {
candidates = [];
for (var i = 0; i < current.length; i++) {
var start = current.slice(0, i);
var end = current.slice(i+1,current.length);
for (j = 1; j <= current.length; j++) {
var c = start.concat([(Math.floor((Math.random()*current.length)+1))].concat(end));
candidates.push(c);
}
}
return candidates;
};
// Generate a random new state for the N Queens problem of size n
var generateState = function(n) {
state = [];
for(var i = 0; i < n; i++){
state[i] = Math.floor(Math.random() * n + 1);
}
return state;
};
// Helper Function to tell us if our configuration is a solution.
var isSolution = function (config) {
return (evaluate(config) === 0);
};
// Workhorse function that solves our puzzle.
var nQueensBestFirstHillClimbing = function (start) {
var best = start;
var current;
var currentEval = evaluate(start);
while (true) {
current = best;
var candidates = generateCandidates(current);
for (var i in candidates){
var candidateEval = evaluate(candidates[i]);
// Lower evaluation number is better for our implementation
if (candidateEval < currentEval) {
current = candidates[i] ;
currentEval = candidateEval;
}
}
// If current & best are STILL the same, then we reached a peak.
if (best == current)
return best;
best = current;
}
};
// Solve the N Queens problem using Random Restart Hill Climbing.
var solveNQueens = function(state) {
count = 1;
state = nQueensBestFirstHillClimbing(state);
while (!isSolution(state)){
// Random Restart If not a Solution.
state = generateState(state.length);
count++;
state = nQueensBestFirstHillClimbing(state);
}
// Return the Number of Hill Climbing Random Restarts & the SOlution.
return [count, state];
};Running The Solver
// Running the Solver for: 4 Queens
solveNQueens(generateState(4));
// or pass in a state to start from.
solveNQueens([1,2,3,4]);
// Running the Solver for: 8 Queens
solveNQueens(generateState(8));
solveNQueens([1,2,3,4,5,6,7,8]);Quick and Dirty Analysis
Since random restart generates random state to start from at each restart, we can only analyze the algorithm in respect to the number of restarts.
For the 8-Queens problem, a sample of 100 runs generated an average of 16.82 Random Restarts, with 13 being the median. This means that our algorithm found a solution only after it has restarted an average of 17 (Rounded Up) times.
Here is what the distribution looks like for 100 8-Queens Problems solved using the Algorithm Above.
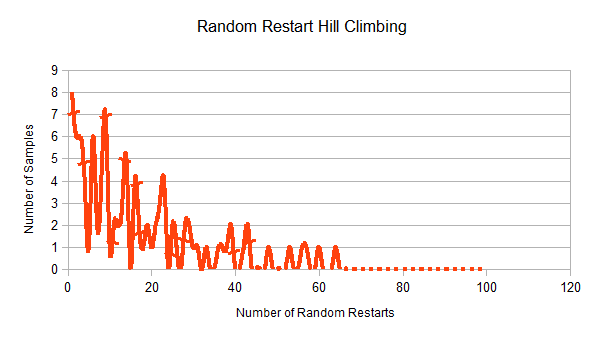
The x-axis is the number of random restarts that any given iteration went through. The y-axis is the number of independent instances that had a given amount of random restarts.